X^2 y^2 z^2=1 graph 275851-Match the equation with its graph x^2-y^2+z^2=1

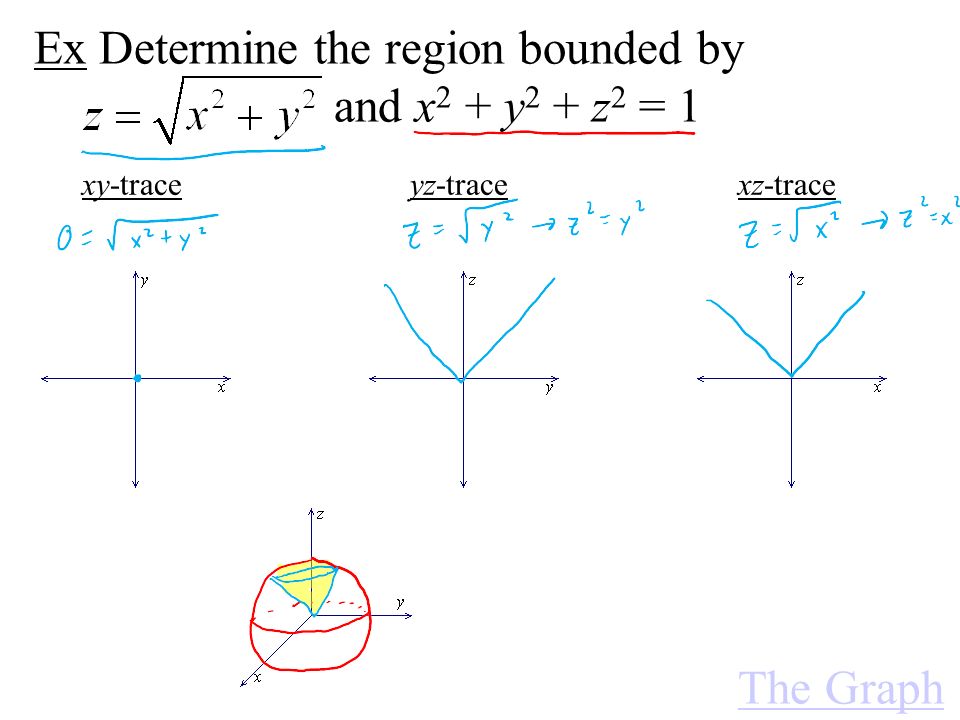
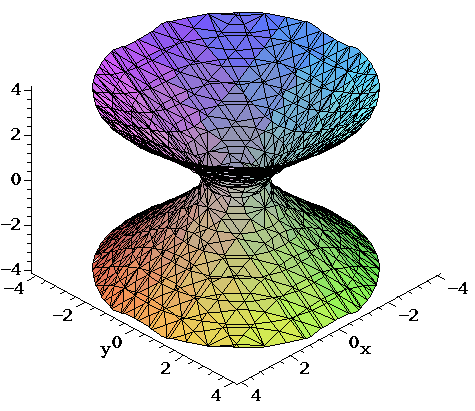
Plane z = 1 The trace in the z = 1 plane is the ellipse x2 y2 8 = 1, shown below 6Their defining characteristic is that their intersections with planes perpendicular to any two of the coordinate axes are hyperbolas There are two types of hyperboloids the first type is illustrated by the graph of x 2 y 2 z 2 = 1, which is shown in the figure below As the figure at the right illustrates, this shape is very similar to the one commonly used for nuclear power plant cooling2 The graph of (x 3)2 (y2)2 (z 1)2 = 16 is a of radius centered at 3 The shortest distance from the point (4, 0, 5) to the sphere (x 1)2 (y 2)2 z = 36 is 4 Let S be the graph of x² 2?

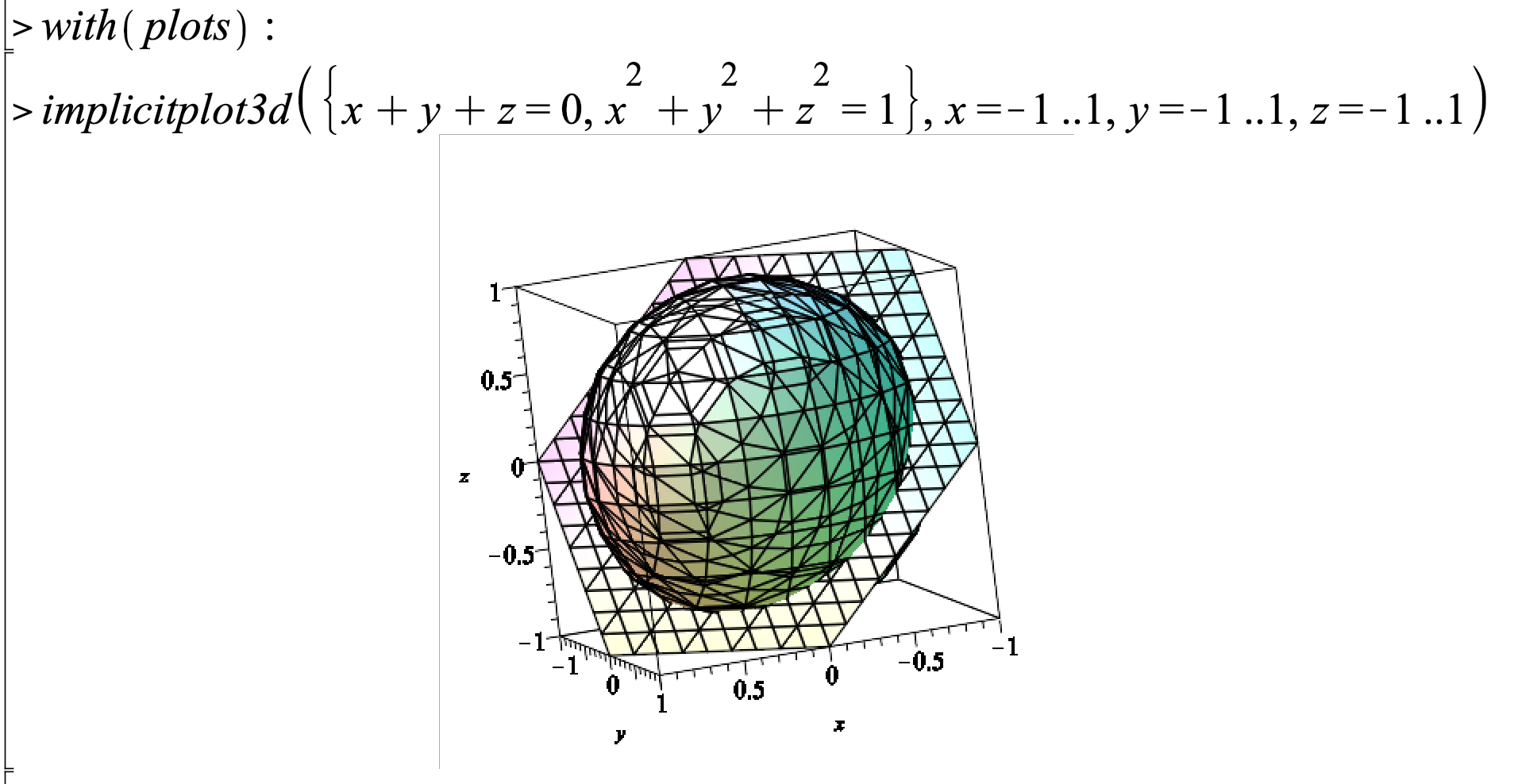
How Do I Plot A Function Under Some Constrainets Mapleprimes

Match the equation with its graph x^2-y^2+z^2=1

Match the equation with its graph x^2-y^2+z^2=1-Plot x^2 3y^2 z^2 = 1 Natural Language;3D plot x^2y^2z^2=4 Natural Language;

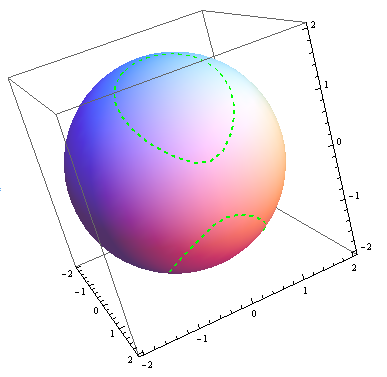
Plotting 3d Surface Intersections As 3d Curves Online Technical Discussion Groups Wolfram Community

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Graph x^2y^2=25 x2 y2 = 25 x 2 y 2 = 25 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k k represents the yoffset from originGraph (x^2)/2(y^2)/2=1 Multiply each term on both sides of the equation by This is the form of a circle Use this form to determine the center and radius of the circle Match the values in this circle to those of the standard form

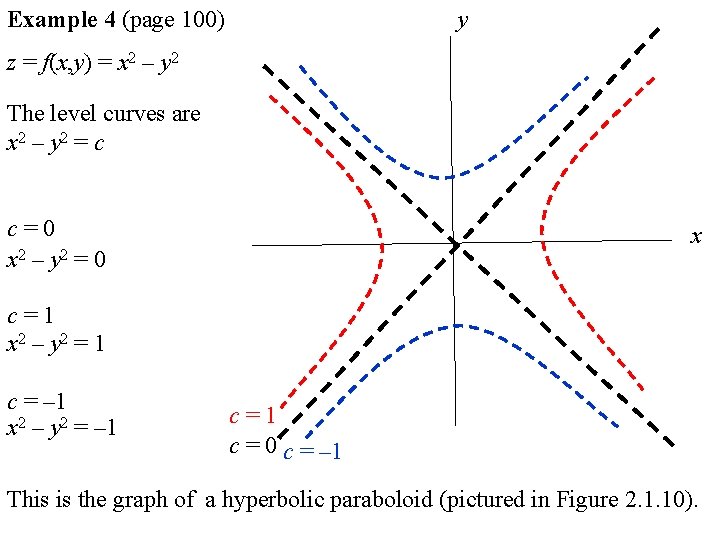
Example 1 Let f ( x, y) = x 2 − y 2 We will study the level curves c = x 2 − y 2 First, look at the case c = 0 The level curve equation x 2 − y 2 = 0 factors to ( x − y) ( x y) = 0 This equation is satisfied if either y = x or y = − x Both these are equations for lines, so the level curve for c = 0 is two lines If you Alternatively, use the $(\vert y \vert, \text{arg}(y))$ cylinder, let $\arg(x)$ again correspond to hue, and let $\vert x \vert$ correspond to brightness or saturation There are other ways of doing this too of course, the idea is that you can pack one, two, or even three dimensions (think RGB) into the color A circle with centre at (–1,–2) and radius 2 units (x1)^2(y2)^2=4 (x(–1))^2(y(–2))^2=2^2 How do you find the center and radius of the ellipse with standard equation #x^26xy^28y11=0#?

The graph of mathx^2(y\sqrt3{x^2})^2=1/math is very interesting and is show below using desmosExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music graph{x^21 10, 10, 5, 5} The last number is the yintercept 1, in this case, so (0,1) can be plotted The yvalues for both x=1 and x=1 are 11, which is 2, so (1,2) and (1,2) can be plotted This is the same for 2 and 2, where (2,4) and (2,4) can be plotted, and so on (Note that there are no negative yvalues)

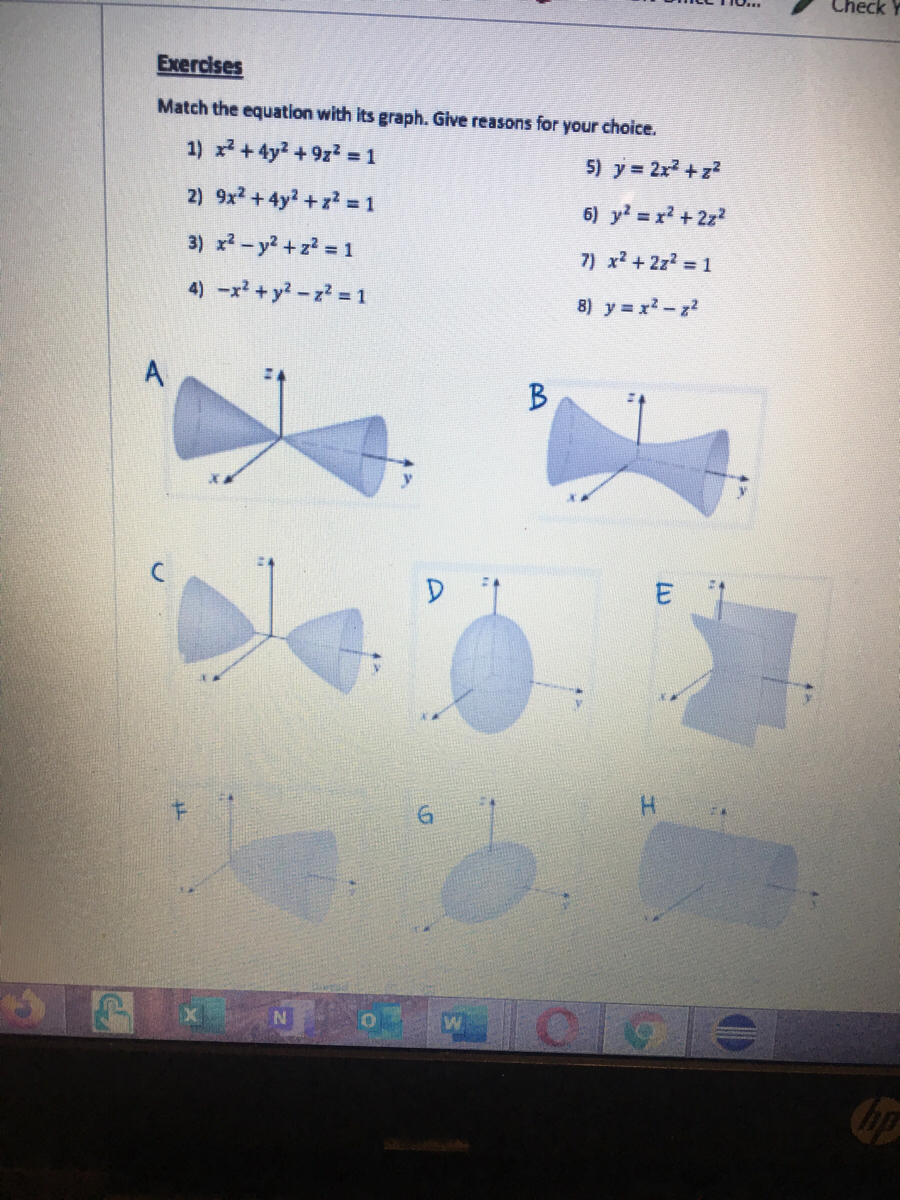
Answered Exercises Match The Equation With Its Bartleby

What Is The 3 D Graph Of X 2 Y 2 Z Where Z 1 And 3 D Graph Of X 2 Y 2 1 What Is The Difference Between Two Of Them Quora

In this math video lesson, I show how to graph the absolute value function y=abs(x2) Absolute value equations can be difficult for students in Algebra 1 i how can i draw graph of z^2=x^2y^2 on matlab Follow 78 views (last 30 days) Show older comments Rabia Kanwal on Vote 0 ⋮ Vote 0 Commented Walter Roberson on Accepted Answer Star Strider 0 Comments Show Hide 1 older comments Sign in to comment Sign in to answer this questionActually, using wolfram alpha to graph it, I cant see where the center is and where the yaxis and zaxis and xaxis are $\endgroup$ – nany Jan 26 '15 at 235

Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download

Section 9 1 Three Dimensional Coordinate Systems X 2 Y 2 Z Sx 2 Y 2 Z 2 2 Xy Plane It Is Sketched In Figure Pdf Free Download

 3D and Contour Grapher A graph in 3 dimensions is written in general z = f(x, y)That is, the zvalue is found by substituting in both an xvalue and a yvalue The first example we see below is the graph of z = sin(x) sin(y)It's a function of x and y You can use the following applet to explore 3D graphs and even create your own, using variables x and yFind stepbystep Calculus solutions and your answer to the following textbook question Sketch the graph of the function f(x,y)=(44x^2y^2)^1/2EX 1 Sketch a graph of z = x2 y2 and x = y2 z2 5 A cylinder is the set of all points on lines parallel to l that intersect C where C is a plane curve and l is a line intersecting C, but not in the plane of C l 6 A Quadric Surface is a 3D surface whose equation is of the second degree

Graphing 3d Graphing X 2 Y 2 Z 2 Intro To Graphing 3d Youtube

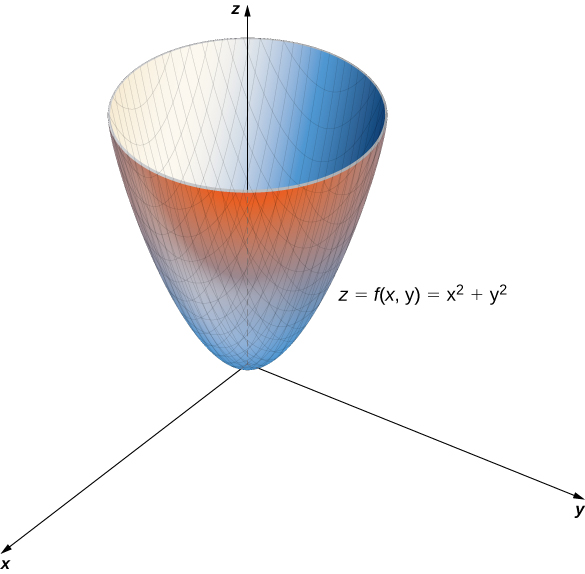
Graphing Functions Of Two Variables By Openstax Jobilize

Math Input NEW Use textbook math notation to enter your math Try itIn this math video lesson I show how to graph y=(1/2)x2 The equation in this video is in slopeintercept form, y=mxb, and is a common way to graph an equHomework Solutions MATH 32B2 (18W) Problem 10 () Sketch the region Dbetween y= x2 and y= x(1 x) Express Das a simple region and calculate the integral of f(x;y) = 2yover D

Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf

Math 138 Fall 18

1) via Wikipedia, the heart shape itself is likely based off the shape of the silphium seed, which was used as a contraceptive, or of course various naughty bits of anatomy And condom sales spike around Vday Relevancy #1 check 2) It's an equation AndX 2 − 2 x y 2 − 2 y z 2 1 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2 for b, and z^ {2}\left (y1\right)^ {2} for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation is in standard form a x 2 b x c = 0412 Sketch a graph of a function of two variables In the first function, (x, y, z) (x, y, z) represents a point in space, and the function f f maps each point in space to a fourth quantity, such as temperature or wind speed In the second function,

Multivariable Functions Application Center

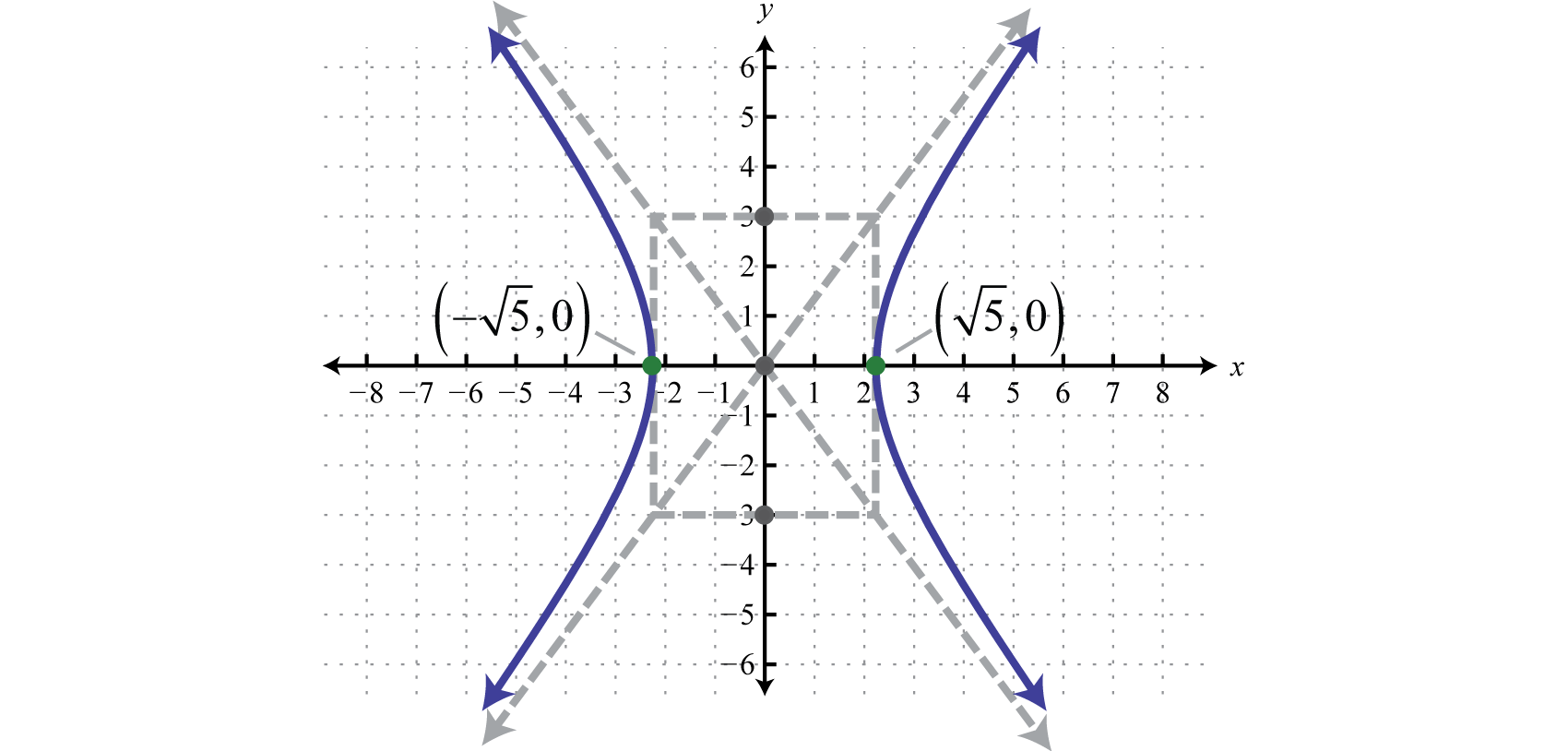
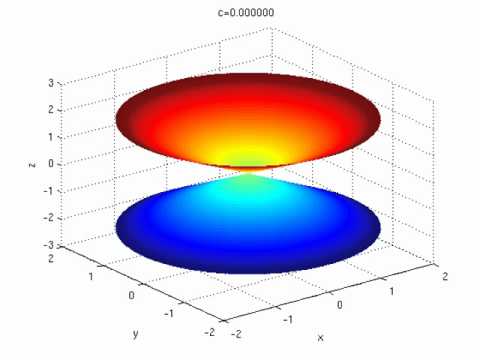
Hyperbolas

(ii) The Graph Of 3 = X^2 2y^2 2 1 Both (i) And (ii) Are Counter Maps 2 Both (i) And (ii) Are Contour Maps 3 (i) Is A Level Curve, And (ii) Is A Counter Map 4 (ii) Is A Level CurveZ = 1/ (X Y) Therefore the given equation becomes X^2 Y^2 1/ (X^2 Y^2) = X Y 1/ (X Y) Solving this equation for Y we have Y = 1/4 {1 Sqrt (A) Sqrt 2 B 2 Sqrt (A)} where A = 1 8/X 4 X 4 X^2 and B = 1 4/X 2 X 2 X^2 If we want real solutions, the only solution for Y is when X = 1WolframAlpha brings expertlevel knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels

Implicit Differentiation

Level Surfaces

Okay, so we have mathz = x^2 y^2/math describing the paraboloid and we have mathx^2 y^2 = 2y/math describing the cylinder That's how they look like together We want the equation describing the cylinder to be in its conventional formGraph x=1y^2 Reorder and Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabolaSee the answer Show transcribed image text Expert Answer 100% (2 ratings) Previous question Next question Transcribed Image Text from this Question

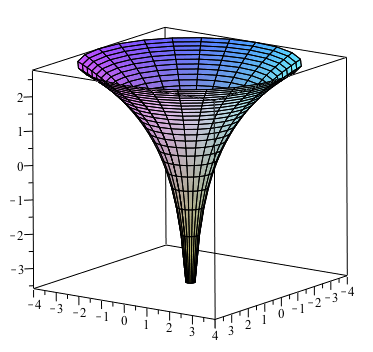
How Do You Sketch F X Y Ln X 2 Y 2 Socratic

Http Web Mnstate Edu Jamesju Fall11 Content M323exam3f11prackey Pdf

ContourPlot3Dx^2 y^2 == 1, {x, 2, 2}, {y, 2, 2}, {z, 2, 2} Share Improve this answer Follow answered Sep 16 '12 at 2247 Mark McClure Mark McClure 315k 3 3 gold badges 97 97 silver badges 156 156 bronze badges $\endgroup$ 2 $\begingroup$ Oh, great!Question Match The Equation With Its Graph X^2 Y^2 Z^2 = 1 Match The Equation With Its Graph x^2 Y^2 Z^2 = 1 This problem has been solved!In the twodimensional coordinate plane, the equation x 2 y 2 = 9 x 2 y 2 = 9 describes a circle centered at the origin with radius 3 3 In threedimensional space, this same equation represents a surface Imagine copies of a circle stacked on top of each other centered on the zaxis (Figure 275), forming a hollow tube

Match The Equations Of The Surface With The Graphs Chegg Com

How To Draw Y 2 X 2 Interactive Mathematics

$\endgroup$ – diracdeltafunk Sep 16 '12 at 22526z = 16 in 3spaceIf one of the variables x, y or z is missing from the equation of a surface, then the surface is a cylinder Note When you are dealing with surfaces, it is important to recognize that an equation like x2 y2 = 1 represents a cylinder and not a circle The trace of the cylinder x 2 y = 1 in the xyplane is the circle with equations x2 y2

X 2 Y 2 Z 2 0 Graph Dawonaldson

Level Surfaces

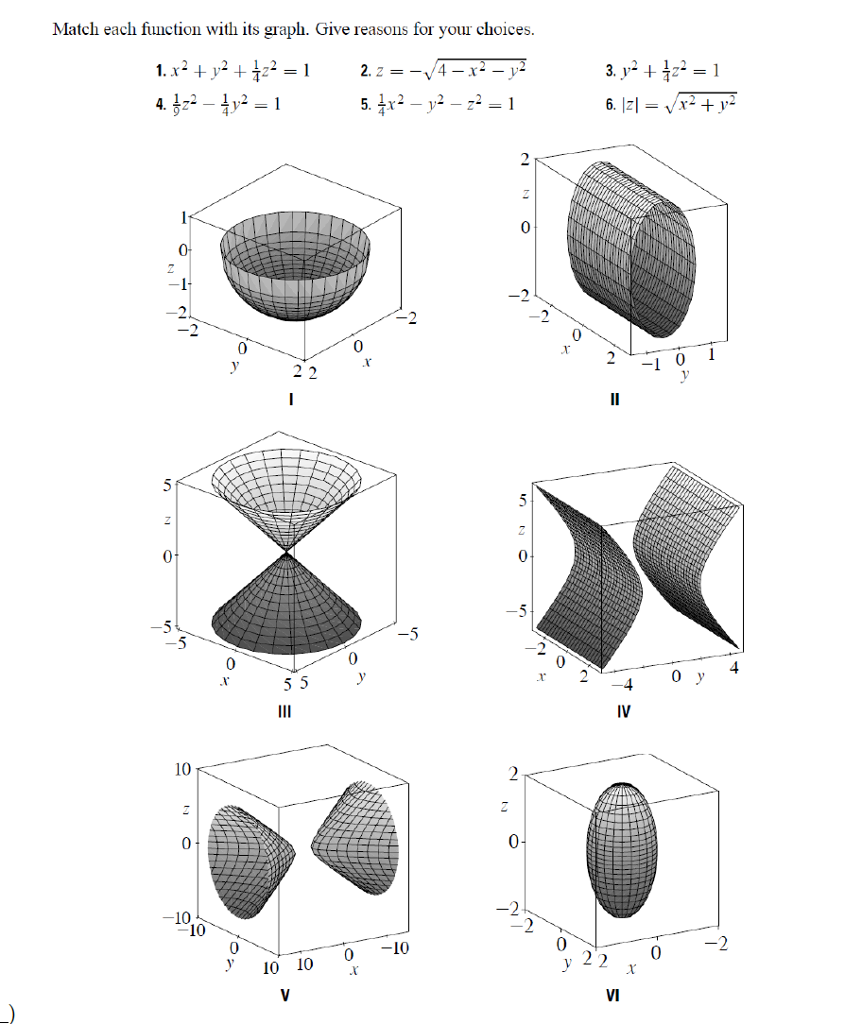
Level surfaces For a function $w=f(x,\,y,\,z) \, U \,\subseteq\, {\mathbb R}^3 \to {\mathbb R}$ the level surface of value $c$ is the surface $S$ in $U \subseteqPreAlgebra Graph x^2y^2=1 x2 − y2 = −1 x 2 y 2 = 1 Find the standard form of the hyperbola Tap for more steps Flip the sign on each term of the equation so the term on the right side is positive − x 2 y 2 = 1 x 2 y 2 = 1 Simplify each term in the equation in order to set the right side equal to 1 1Xz plane traces create ellipses This tells us the surface is an ellipsoid because there are 2 ellipsoid graphs to choose from, we look at the major axis in the function and pick the graph with the corresponding major axis x axis radius = 1, y axis radius = (sqrt (1/4))^2 z axis radius = (sqrt (1/9))^2 We see the major axis is the x axis, and the corresponding graph is VII

Scarpelli Assignment 2

Surfaces Part 2

Math Input NEW Use textbook math notation to enter your math Try itTo graph the XY plane you set Z = 0 and plot the function as you normally would, so z = (x 2 y 2 − 1) == 0 = (x 2 y 2 − 1) Therefore x 2 y 2 = 1 is your XY axis graph, which is just a circle of radius 1 centered at the origin $\begingroup$ why would yaxix and zaxis be parallel ?

How To Plot Equation X 2 Y 2 1 3 X 2 Y 3 Stack Overflow

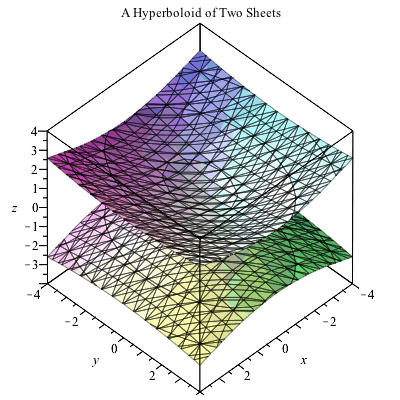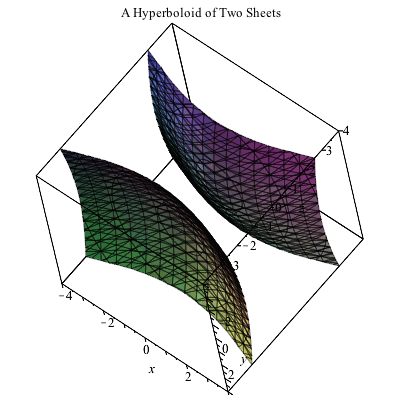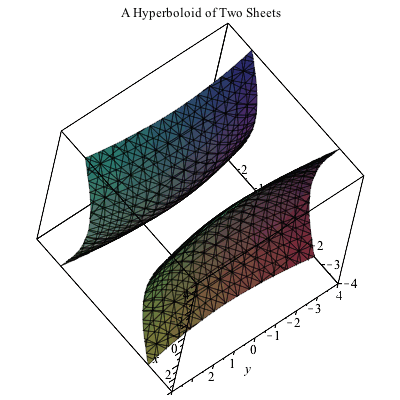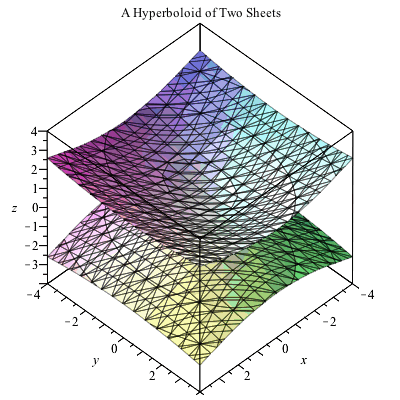
Plotting In 3d

Steps to graph x^2 y^2 = 4When z = x 2 y 2, the trace on y = b is the graph of z = x 2 b 2, while that on x = a is the graph of z = a 2 y 2;(e) Below is the graph of z = x2 y2 On the graph of the surface, sketch the traces that you found in parts (a) and (c) For problems 1213, nd an equation of the trace of the surface in the indicated plane Describe the graph of the trace 12 Surface 8x 2 y z2 = 9;

1

What Is The Graph Of X 2 Y 3 X 2 2 1 Quora

 A quick video about graphing 3d for those who never done it before Pause the video and try itIf the point lies on the surface z = 8−x2−y2, then the distance is the following function on x and y f(x,y) = 2x2y 8−x2 − y2 3 Where the surface lies above the plane the function f(x,y) is positive Taking the partial derivatives and setting them equal to 0, f x(x,y) = (2− 2x)/3 = 0, f y(x,y) = (2−2y)/3 = 0, gives x = y = 12x2y=4 Geometric figure Straight Line Slope = 1 xintercept = 2/1 = 0000 yintercept = 2/1 = 0000 Rearrange Rearrange the equation by subtracting what is to the right of the

1

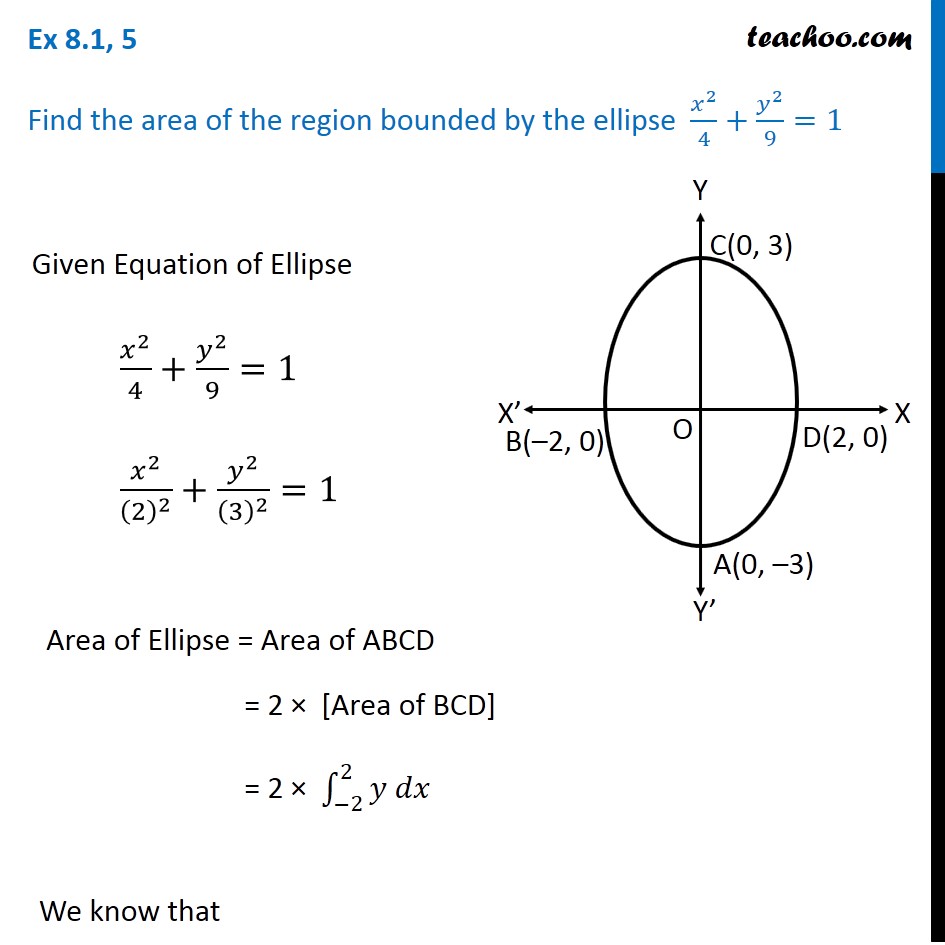
Ex 8 1 5 Find Area By Ellipse X2 4 Y2 9 1 Class 12

 The graph of a function f (x,y) is the set of all points (x,y,z) in space such that (x,y) is in the domain of f and z=f (x,y) Here are a few examples Example 1 f (x,y) = x 2 y 2 Example 2 f (x,y) = x 2 y 2 Example 2 f (x,y) = e x2y2 Example 3Graph x^2y=1 x2 − y = 1 x 2 y = 1 Solve for y y Tap for more steps Subtract x 2 x 2 from both sides of the equation − y = 1 − x 2 y = 1 x 2 Multiply each term in − y = 1 − x 2 y = 1 x 2 by − 1 1 Tap for more steps Multiply each term in − y = 1 − x 2 y = 1 x 2 by − 1 1This preview shows page 1 3 out of 3 pages Graph (a) x 2 y 2 9 z 2 16 = 1 HYPERBOLOIDOF ONESHEET (a) − x 2 a 2 y 2 b 2 − z 2 c 2 = 1 (b) x 2 a 2 − y 2 b 2 z 2 c 2 = 1 (c) x 2 a 2 y 2 b 2 − z 2 c 2 = 1 1 − Theequationhas onenegative variable 2 − Every variablehasa power of 2 3The equationhasaconstant Thehyperboloids alwaystraveled alongtheaxis with negativesign

Graph Graph Equations With Step By Step Math Problem Solver

Homework 3 Model Solution Han

 Explanation The equation of a circle is given by (x −h)2 (y −k)2 = r2 with center (h,k) and radius r We have the equation x2 y2 = 100, where the origin is our center since we have no h or k value We also know from √100 that we have radius 10 We can now graph this circle knowing we are centered at the origin, and we have a radius1 This figure is the (double) cone of equation x 2 = y 2 − z 2 The gray plane is the plane ( x, y) You can see that it is a cone noting that for any y = a the projection of the surface on the plane ( x, z) is a circumference of radius a with equation z 2 x 2 = a 2The Graph Of Z F(x,y)= X^2 2y^2 2;

Visualizing Functions Of Several Variables And Surfaces

Software To Display 3d Surfaces Newbedev

These are parabolas which always opening upwards On the other hand the horizontal trace on z = c is the circle x 2 y 2 = c So this surface is called a Paraboloid You can think of it as a crater or a wineglass!

Parameterized Surfaces 2 Html

Plot A Graph Of The Equation Y 2 X 2 2z 2 Study Com

2 D And 3 D Plots Matlab Simulink

Plotting Surfaces Colgate Pages 1 4 Flip Pdf Download Fliphtml5

Graph It Aka Graph It Ii Schaubild Aka Graph It Enhanced Atarinside

Graph X 2 Ky 2 25 For Different Values Of K

Levelset Html

Z 1 1 Z 2 1 For Bvp X X 3 5p 2 2 X X 0 X 1 0 U 0 Download Scientific Diagram

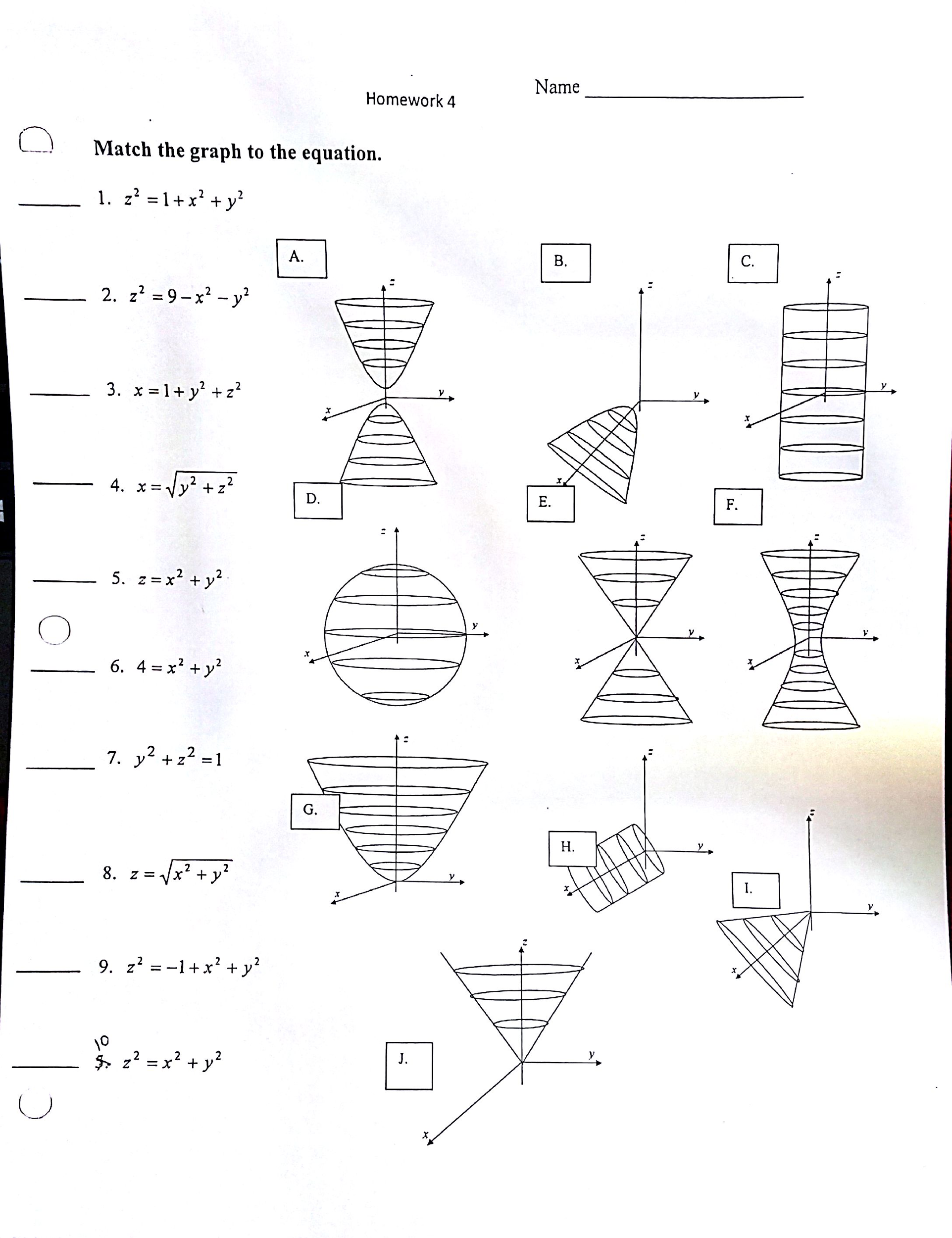
Match The Graph To The Equation X 2 1 X 2 Y 2 Chegg Com

How Do I Reproduce This Heart Shaped Mesh In Matlab Stack Overflow

Draw The Graphs Of The Following Equations 3x Y 2 0 And 2x Y 8 0 On The Graph Paper Ii Brainly In

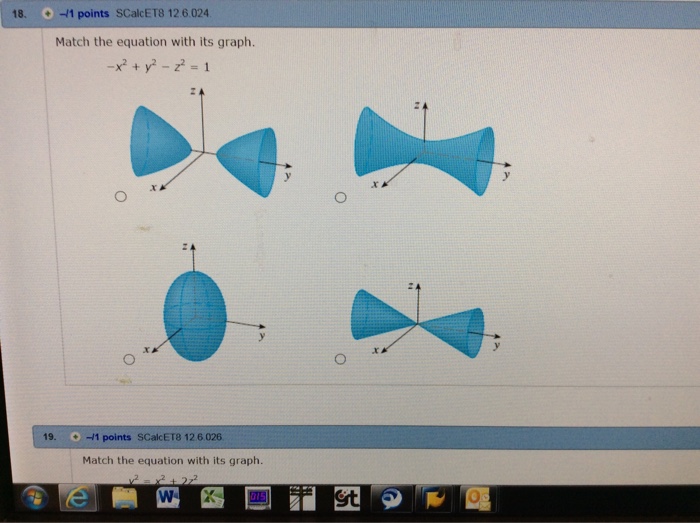
Match The Equation With Its Graph X 2 Y 2 Z 2 Chegg Com

Find The Volume Inside Both The Cylinder X 2 Y 2 1 And The Sphere X 2 Y 2 Z 2 4 Study Com

Solved Graph The Solid That Lies Between The Surface Z 2xy X 2 1 And The Plane Z X 2y And Is Bounded

Draw The Graph Of The Surface Given By Z 1 2 Sqrt X 2 Y 2 Study Com

Multiple Integrals1 Html

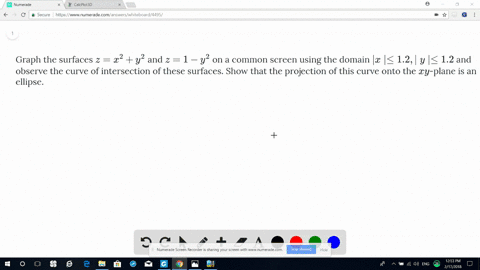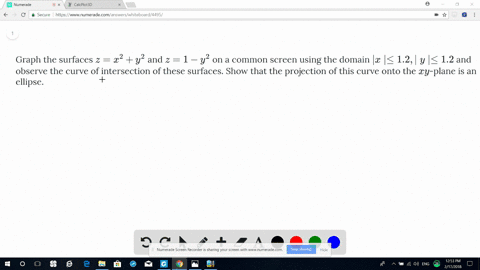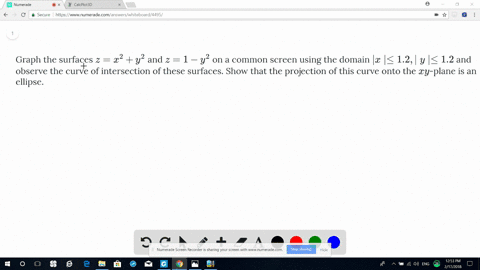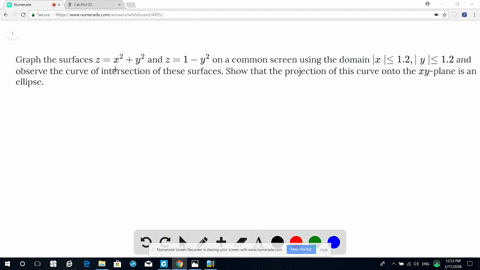
Solved Graph The Surfaces Z X 2 Y 2 And Z 1 Y 2 On A Common Screen Using The Domain Mid X Mid Le 1 2 Mid

Lesson 10 Functions And Level Sets

The Solid E Bounded By The Equation 9 X 2 4 Y 2 Z 2 1 And Located The First Octant Is Represented In The Following Figure A Trite

If X X 1 X 2 Represents

Algebra 2 C70 Kla Sefinar L See How To Solve It At Qanda

How Do I Plot A Function Under Some Constrainets Mapleprimes

印刷可能 X2 Y2 Z21 Graph シモネタ

How To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange

T 2 1 Now The Set Of Vertices X 1 Y 1 Z 1 X Y Z Induces A Download Scientific Diagram

Multivariable Functions Application Center

Cylinders And Quadratic Surfaces A Cylinder Is The Continuation Of A 2 D Curve Into 3 D No Longer Just A Soda Can Ex Sketch The Surface Z X Ppt Download

Surfaces Part 2

Quadratics Graphing Parabolas Sparknotes

Saddle Point Wikipedia

Match Each Function With Its Graph Give Reasons For Chegg Com

Multiple Integrals H 2 Y Are Continuous Functions On C D And Let F X Y Be A Function Defined On R Then Pdf Free Download

3dplotting

Quadratics Graphing Parabolas Sparknotes

Graph X 2 Y 2 4 Youtube

3d Surface Plotter Academo Org Free Interactive Education

Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits

1

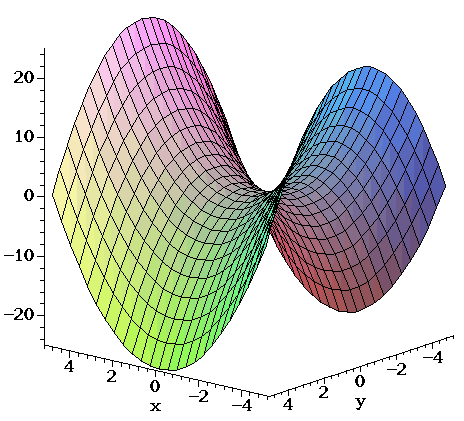
Surfaces Part 2

Find The Volume Of The Solid Bounced By The Planes Z 0 Z Y And X 2 Y 2 1 Mathematics Stack Exchange

Quadricsurfs Html

Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework11 7 Ans Pdf

How To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange

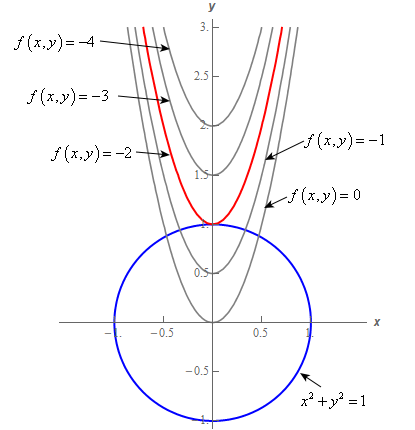
Calculus Iii Lagrange Multipliers

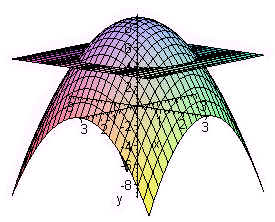
Math 2 Midterm 2

Multivariatefunctions Html

Gnuplot Demo Script Singulr Dem

Analiticheskaya Geometriya V Prostranstve

Ellipsoid

How To Draw Y 2 X 2 Interactive Mathematics

Equation Of A Sphere Graph Physics Forums

Surfaces Part 2

13 1 Functions Of Several Variables Mathematics Libretexts

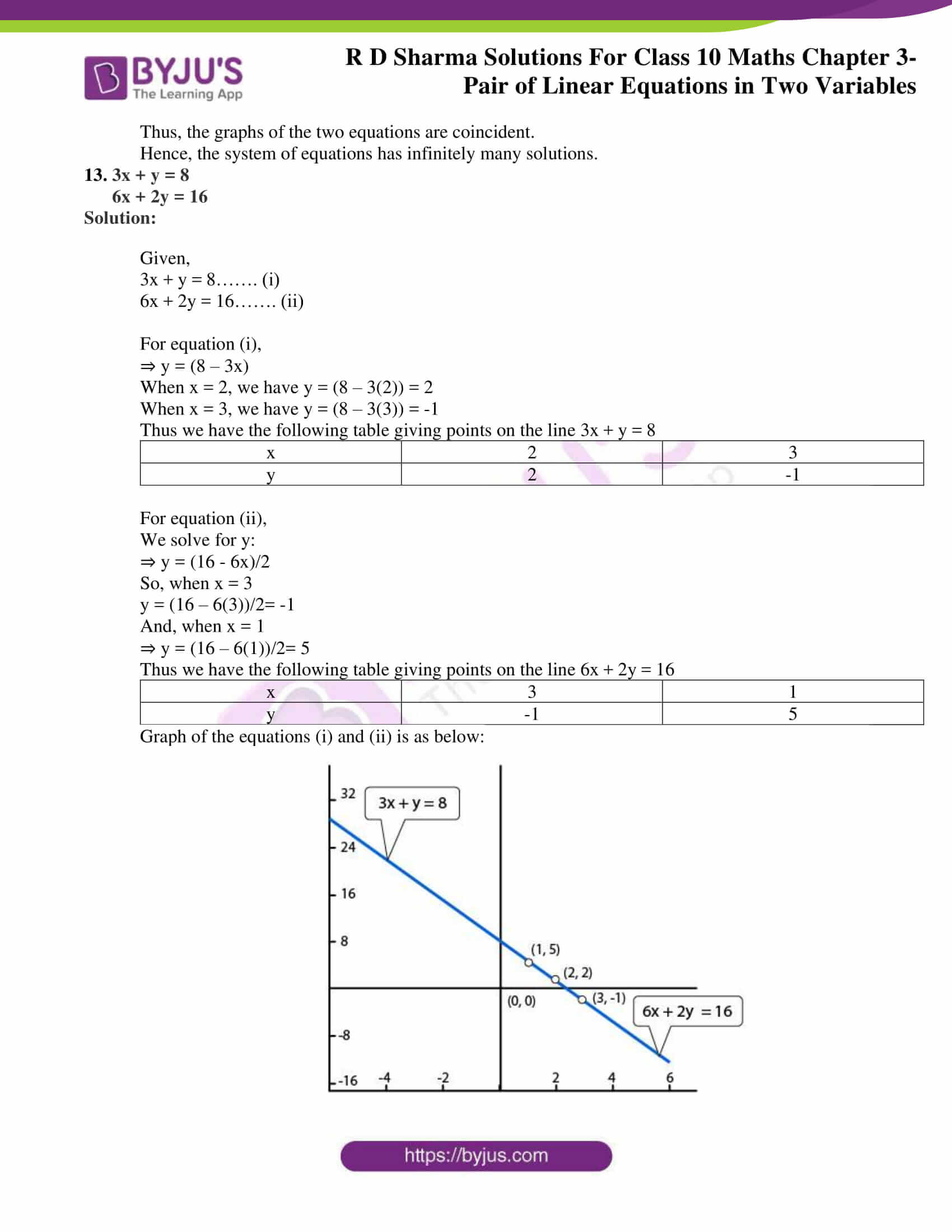
Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2

Graph The Cylinder X 2 Y 2 16 And The Sphere X 2 Y 2 Z 2 49 Together Using Maple And Find The Volume Outside The Cylinder And Inside The Sphere Study Com

Level Sets Math Insight

What Is The Graph Of X 2 Y 2 Z 2 1 Quora

Plotting 3d Surface Intersections As 3d Curves Online Technical Discussion Groups Wolfram Community

Does Anyone Know How To Graph X 2 2y 2 3z 2 12 Mathematics Stack Exchange

70以上 Y2x2 Z2 ニスヌーピー 壁紙

Beka Z Mat Fizu Wesolych 1 2 Sqrt 1 Sqrt X 2 Y 2 2 1 X 2 Y 2 Sin 10 X 3 Y 5 7 1 4 From 1 6 To 1 6 Facebook

23 Match The Equation X 2 Y 2 Z 2 1 With Its Graph Labeled I Viii Toughstem

Gnuplot Demo Script Singulr Dem

Which Graph Represents The Solution To The System Of Equations X 2y 4 2x Y 1 2 A Top Brainly Com

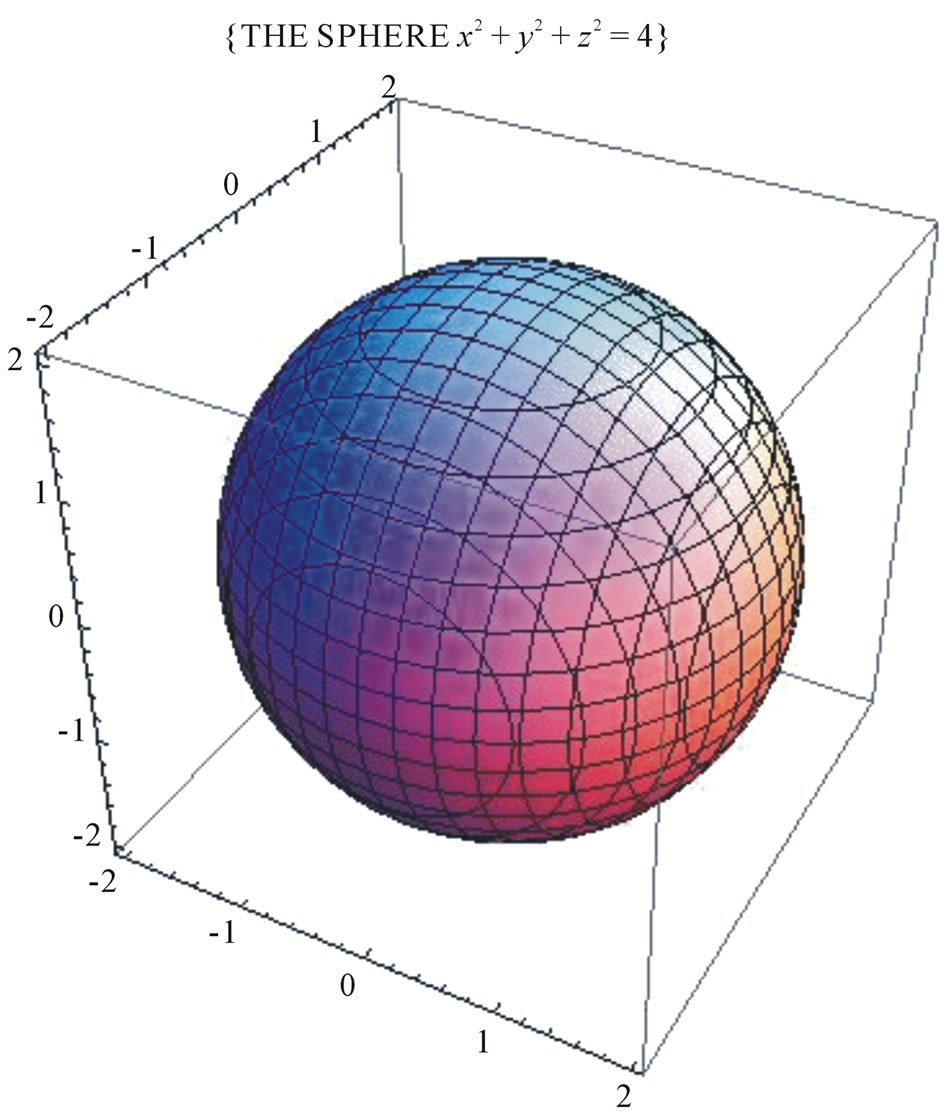
Some Examples To Show That Objects Be Presented By Mathematical Equations

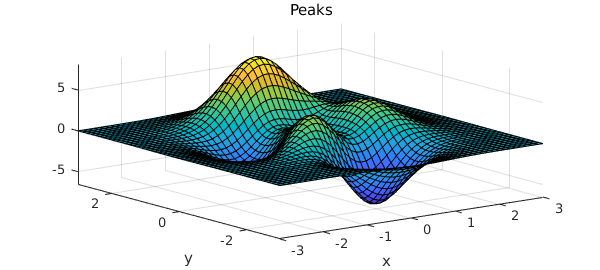
12 Chebfun2 Getting Started Chebfun

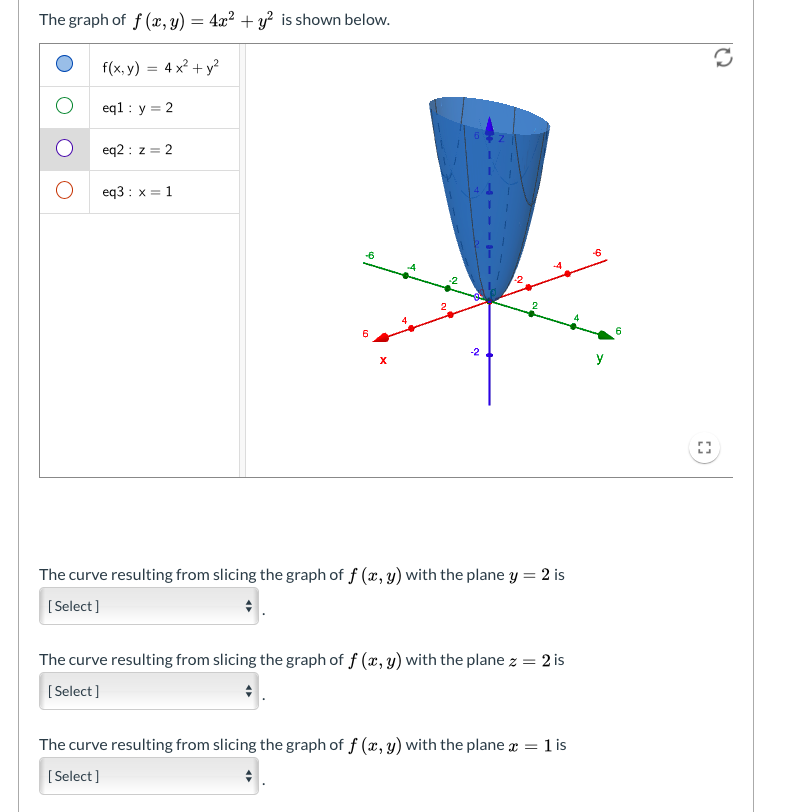
The Graph Of F X Y 4 X2 Y2 Is Shown Below Chegg Com

How Do You Graph X 2 Y 2 1 Socratic

Graficos 3d Application Center

Drawing Cylinders In Matlab

Implicit Differentiation

Matlab Tutorial

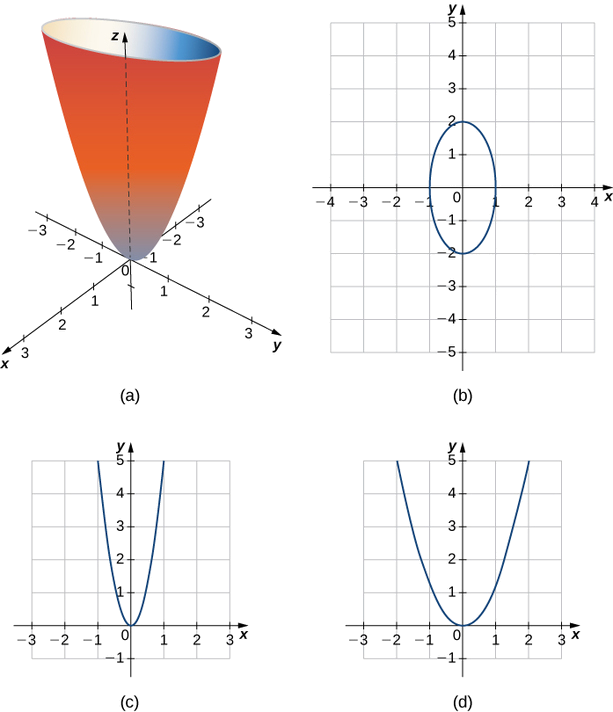
12 6 Quadric Surfaces Mathematics Libretexts

X 2 Y 2 Graph

Incoming Term: x^2+y^2+z^2=1 graph, x^2+y^2+z^2=1 plot, plot x^2+y^2+z^2=1 in matlab, match the equation with its graph x^2-y^2+z^2=1,